분할 정복
종이의 개수 & 하노이 탑
4gats
2023. 8. 16. 14:35
https://www.acmicpc.net/problem/1780
1780번: 종이의 개수
N×N크기의 행렬로 표현되는 종이가 있다. 종이의 각 칸에는 -1, 0, 1 중 하나가 저장되어 있다. 우리는 이 행렬을 다음과 같은 규칙에 따라 적절한 크기로 자르려고 한다. 만약 종이가 모두 같은 수
www.acmicpc.net
- 만약 종이가 모두 같은 수로 되어 있다면 이 종이를 그대로 사용한다.
- (1)이 아닌 경우에는 종이를 같은 크기의 종이 9개로 자르고, 각각의 잘린 종이에 대해서 (1)의 과정을 반복한다
분할 정복을 써야할 거 같다.
void solve(int x, int y, int n)
{
if (same(x, y, n))
{
cnt[a[x][y] + 1] += 1;
return;
}
int m = n / 3;
for (int i = 0; i < 3; i++)
{
for (int j = 0; j < 3; j++)
{
solve(x + i * m, y + j * m, m);
}
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
|
#include <iostream>
using namespace std;
int a[3000][3000];
int cnt[3];
bool same(int x, int y, int n)
{
for (int i = x; i < x + n; i++)
{
for (int j = y; j < y + n; j++)
{
if (a[x][y] != a[i][j])
return false;
}
}
return true;
}
void solve(int x, int y, int n)
{
if (same(x, y, n))
{
cnt[a[x][y] + 1] += 1;
return;
}
int m = n / 3;
for (int i = 0; i < 3; i++)
{
for (int j = 0; j < 3; j++)
{
solve(x + i * m, y + j * m, m);
}
}
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int n;
cin >> n;
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
cin >> a[i][j];
}
}
solve(0, 0, n);
for (int i = 0; i < 3; i++) {
cout << cnt[i] << '\n';
}
return 0;
}
|
cs |
https://www.acmicpc.net/problem/11729
11729번: 하노이 탑 이동 순서
세 개의 장대가 있고 첫 번째 장대에는 반경이 서로 다른 n개의 원판이 쌓여 있다. 각 원판은 반경이 큰 순서대로 쌓여있다. 이제 수도승들이 다음 규칙에 따라 첫 번째 장대에서 세 번째 장대로
www.acmicpc.net
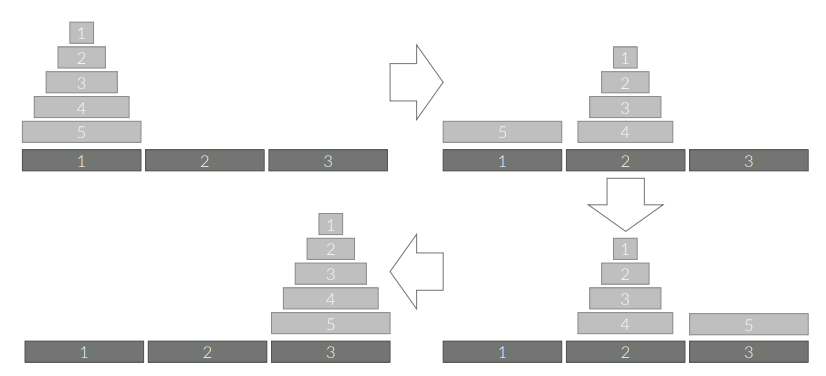
5를 옮기기 위해서는 위에 원판들을 2번으로 옮겨야한다.
solve(n - 1, x, 6 - x - y);
그리고 5를 옮긴다.
그리고 위에 원판들을 3번으로 옮긴다.
solve(n - 1, 6 - x - y, y);
점화식을 만들어보자
d[1] = 1
d[n] = d[n-1] + 1 + d[n - 1]
= 2 * d[n-1] + 1
양변에 1을 더하자
d[n] + 1 = 2 (d[n-1] + 1)
치환
e[n] = 2 * e[n-1]
e[1] = 2
e[n] = 2 ^ n
고로 d[n] = 2 ^ n - 1 which is equal with (1 << n) - 1
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
#include <iostream>
using namespace std;
// n개의 원판을 x번탑에서 y번탑으로 이동시키는 함수
void solve(int n, int x, int y)
{
if (n == 0) return;
// n을 옮기기 위해서는 위의 n - 1개가 이동해야함
// why? 6 - x - y : x와 y가 아닌 다른 곳
solve(n - 1, x, 6 - x - y);
cout << x << ' ' << y << '\n';
solve(n - 1, 6 - x - y, y);
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int n;
cin >> n;
cout << (1 << n) - 1 << '\n';
solve(n, 1, 3);
return 0;
}
|
cs |